Radiciação e suas propriedades .

Definição:

Esta imagem representa a raiz cúbica de oito. A expressão matemática 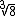 é um radical, ela é composta pelo número 3 que é o índice da raiz, pelo símbolo da radiciação e pelo número 8 que é o seu radicando.

Mas o que significa a raiz cúbica de oito?

Na potenciação, 2³ é igual a 2 _^. 2 _^. 2 que é igual a 8. Partimos do número 2 e através de uma multiplicação de 3 fatores iguais a 2, chegamos ao número 8. Agora temos o caminho inverso, araiz cúbica de oito é a operação que nos aponta qual é número que elevado a 3 é igual a 8, ou seja, é a operação inversa da potenciação.

Propriedades da Radiciação

As propriedades que vamos estudar agora são consideradas no conjunto dos números reais positivos ou nulos, podendo não se verificar caso o radicando seja negativo, pois como sabemos, não existe raiz real de um número negativo.

Símbolo da Radiciação : 

Este é o símbolo de raiz ou sinal de raiz ou simplesmente radical.

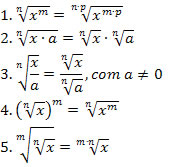
Simplificação de Radiciação : 

Exemplo : 

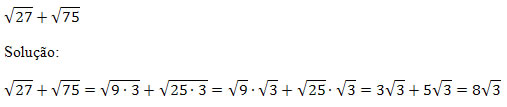
Aplicando as propriedades da Radiciação : 

P1. A raiz enésima do produto a.b é igual ao produto das raízes enésimas de a e b:

               

Demonstração:

Da definição de radiciação, temos que:

                                                                    

P2. O produto das raízes de a e de b com o mesmo índice n é igual a raiz enésima do produto a.b (note que esta propriedade é a recíproca de P1. Nas demais propriedades a recíproca também é válida. Esclarecimentos do que se entende por recíproca você pode obter no artigo sobre Potenciação ) :

                                                                    

P3. O quociente de raízes de mesmo índice n é igual a raiz enésima do quociente dos radicandos:

                          

P4. A potência de grau m da raiz de índice n de a é igual a raíz de índice n de a elevado à potência m:
                           

P5. A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:



P6. A raiz enésima de a elevado a m é igual a raiz de índice p.n de a elevado a p.m obtida multiplicando-se o índice e radicando por p. A mesma propriedade é válida para a divisão:

                  

Simplificação de Radicais Através da Fatoração :

Podemos simplificar e em alguns casos até mesmo eliminar radicais, através da decomposição do radicando em fatores primos. O raciocínio é simples, decompomos o radicando em fatores primos por fatoração e depois simplificamos os expoentes que são divisíveis pelo índice do radicando.

Vamos simplificar 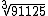decompondo 91125 em fatores primos:

Como 91125 = 3^{6 _.} 5³ podemos dizer que:

 

Repare que tanto o expoente do fator 3⁶, quanto o expoente do fator 5³ são múltiplos do índice do radicando que é igual a 3. Vamos então simplificá-los: